在稳定性实验考察的数据分析中，用的最多的往往是一般线性模型，现在软件选择这么多，该如何区分一些参数呢？下面做简要介绍。

Type：检验的平方和

• I：序贯型，嵌套设计
• II：平衡设计，仅主效应
• III：调整型
• IV：不完整数据

Contrasts(对比):

• Minitab/JMP无此项
• R/SPSS有。

R中: options(contrasts=c(unordered="contr.treatment",ordered="contr.poly"))为默认选项。此选项在方差分析或回归分析建模时，如果有因子，可以使用此参数。第一个是无序因子的参数，第二个是有序因子的参数。同时，也可以通过在建模时指定contrasts参数。比如td_fit<-lm(Potency~Lot*Time,data=td,contrasts = list(Lot="contr.sum"))

• R（系数对比）:
  

首先介绍一下系数对比。

- contr.helmert:
- contr.poly
- contr.SAS: SPSS默认使用此对比方式，设置此项时，R语言返回结果与SPSS的参数估计值相同。
- contr.sum: JMP默认使用此对比方式，设置此项时，R语言返回结果与JMP的协变量，交互效应，截距参数       估计值相同。
- contr.treatment：Minitab默认使用此对比方式，设置此项时，R语言返回结果与Minitab的参数估计值相       同。

• R(方差分析表）

方差分析表来讲，Minitab, JMP, SPSS在模型,误差,合计上一致。但回归项下各主效应和交互效应的平方和不同。

- contr.helmert/contr.sum/contr.poly:设置此项时，R语言返回结果与SPSS的参数估计值相同。
- contr.SAS: 无具体描述
- contr.treatment：无具体描述

结果输出对比 (R vs JMP)

文件下载：

JMP 文件

CSV 数据文件

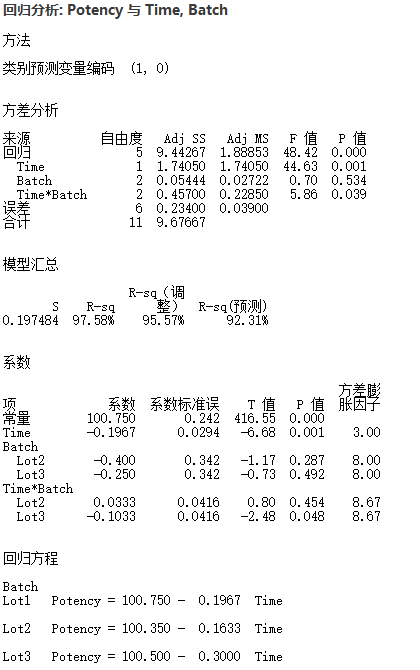
JMP的分析结果如下

R Code

td<-read.csv(”~/regression_interactive.csv”) td$time<-scale(td$Time,scale = FALSE,center = TRUE) td_fit<-lm(Potency~time,data=td,contrasts=list(Batch=“contr.sum”)) summary(td_fit) library(car) Anova(td_fit,type=“III”)

R的分析结果如下

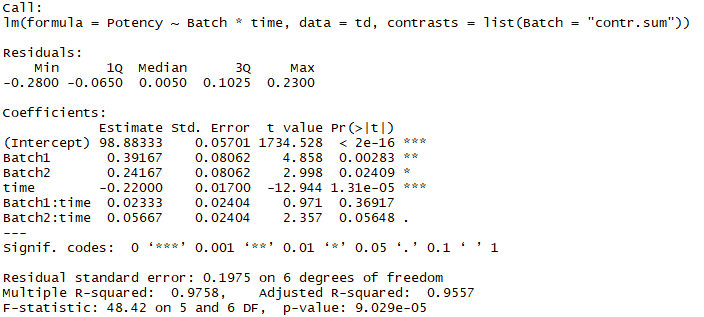
其中，比较重要的是对于无序因子的SS平方和计算的设置，要设置成"contr.sum",另外，应该把Time中心化，然后再拟合模型。

slope=tan(A)=a/b, 其中a是截距变化，b是横坐标变化。

所以，中心化以后，横坐标减掉了7.5，所以截距减少(a)=斜率(slope) x 横坐标变化(b)=-0.22 x 7.5=-1.65，所以真实截距=98.88333-(-1.65)=100.53333。

JMP虽然在计算系数的时候中心化了，但是计算截距的时候，还原成了真实截距。

结果输出对比 (R vs Minitab)

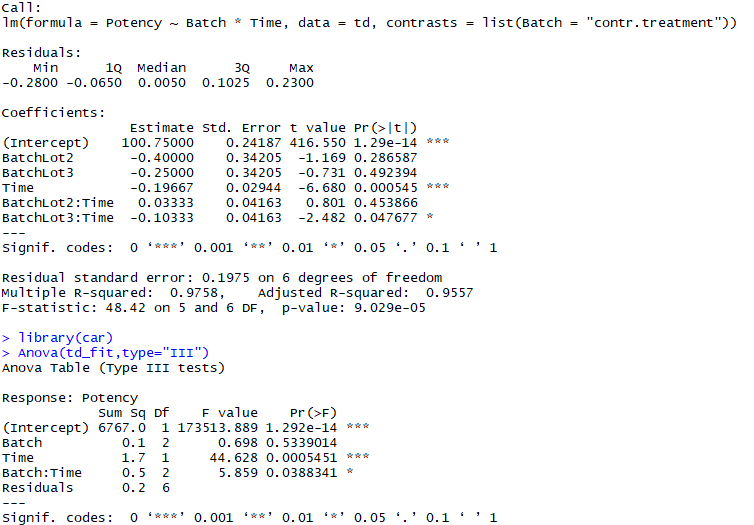
Minitab的分析结果如下

R Code

td<-read.csv(”~/regression_interactive.csv”) td_fit<-lm(Potency~time,data=td,contrasts=list(Batch=“contr.treatment”)) summary(td_fit) library(car) Anova(td_fit,type=“III”)

R的分析结果如下

结果一致。

结果输出对比 (R vs SPSS)

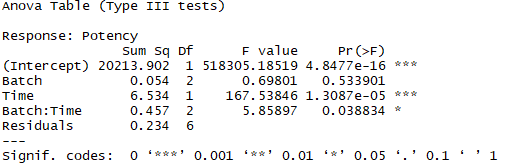
方差分析表

SPSS

R Code

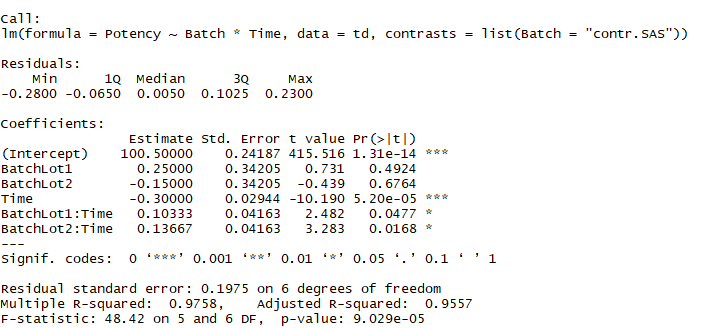
td<-read.csv(”~/regression_interactive.csv”) td_fit<-lm(Potency~Batch*Time,data=td,contrasts=list(Batch=“contr.SAS”)) summary(td_fit)

R Result

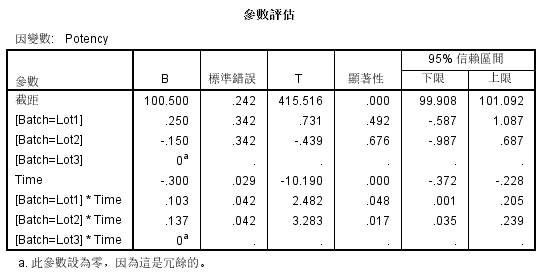
系数表

SPSS

R Code

td_fit2<-lm(Potency~Batch*Time,data=td,contrasts=list(Batch=“contr.helmert”)) library(car) print(Anova(td_fit2,type=“III”),digits=7) #drop1(td_fit2,~.,test=“F”)

R Result